Emergence and Nemetics

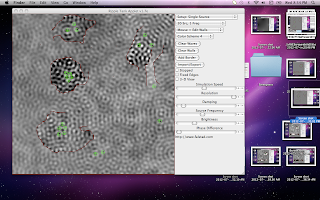
Please excuse the distractions on the right hand side of the figures, just uncropped snaps from my desktop. 

The following series of snapshots of dynamic iterations of wave interactions suggests that emergence can be emulate with a nemetics simulator.  Still much to investigate but the direction seems fruitful. 

The central Nemetical insight was developed by Dibyendu De  He was first to frame Complex Adaptive System as interactions of Red, Green, Blue Waves. The metaphor is best represented in this graph.

The graph can be mapped to reality in many ways. Dibyendu has the experience, insight and talent to map to mathematical rules. 

Consider the square of the figures below as the field of focus. At the top level - the Blue wave  is closed ( indicated by the red boundary on all four sides. Each internal nShape is "open" with different characteristics of "open" in each case. (edges within edges.) 

The points is the source of Events. Each beat of the frequency is an event - the R wave. 

The black and white patterns are the Green wave - observable behavior of wave interactions with in the scale of interest.

Unfortunately the model needs to be modified to be optimize it's ability to model nemetic interactions. One would like the ability to set the frequency of each point independently. One would also like to be able to change the walls while the iterations are playing out.

My conjecture is with these and some other small changes it will be possible to model nemetical interactions at every scale for every Complex Adaptive System.

The Set Up

The red lines and green points are set by hand.
The right hand panel shows the setting of the parameters. 

Figure 1 Time x

Figure 2. Time: x + a

Figure 3, TIme x + a + b

Figure 4. Time x + a + b + c

Figure 5. Time x + a + b + c + d

Figure 6.  Time x + a + b + c + d .....n

End State

Three different 3d Views of End State 

Open v Closed nTubes

Figure 1. The Setup

Two nemitubes have open nTubes. The one on the lower left is closed.

Figure 2. Snapshot a Time X 

The full field is a closed space. Indicated by red borders at the edges.

The Closed nTube has a significantly different pattern.

Figure 3.  Snapshot at Time X + approximately 1 sec.

It's hard to see with only snapshots but the closed nTube in the lower right moves into non linear effects with relatively few iterations.

Figure 4.
The same set up of wave sources, with no walls,  to emulate a perfectly open system.