Consider : NemiString is one of the key concepts of nemetics. What if an Nstring is composed of three kinds of nemes that when joined behave consistent with the maths of wave dynamics.
In this context, Rwave are the events that are Noticed and thus trigger waves of emotion and cognition. It can also be described as What one Sees. It might called the Notice string.
Gwave is as in every nemetic RGB wave model is behavior at the scale of interest. In nemetical terms it is the wave of Exhange.
The Bwave is the nString that captures an evidenced based and critical narrative. One might say the Bwave is similar to what has been called Slow Thinking. In nemetical jargon it might be described as the Engage.Mull string.
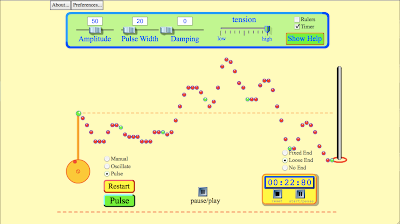
So in the snapshot below. the oval areas mark strings of Rnemes, Gnemes, Bnemes embedded in a a larger nString. The idea is that every nString can be described as R weighted, G weighted and Bwieghted strings. The greater number of R nemes would result in an Rweighted nString. The same definition apples to B and G nemes.
Consider the following snapshot.
After a number of iterations it's a snapshot of a moving wave form. The idea here is that as the overall nString vibrates mini strings quickly appear and disappear. The particular string that separates is described above as GGBR, GGB, and RGB strings.
If we can build a three string model some mechanisms can be studied. My conjecture is the strong force is that like nemes attract. R tends to bind to R, G tends to bind to G, B tend to bind to B.
However, the countervailing force emerges as in the snapshot above as smaller nStrings are "freed" according to the maths of wave mechanics. For example in the GGB string above emits . Two G nemes and One B neme. If the GGB string is in a proximate postion to a BBB string, the chances of successful Exchange as the B emits one and the BBB emits three, the chance of a link being created by persistent neme exchange increases.
If and only if the initial exchange leads to persistent exchange the GGB and BBB strings are pulled closer together. The new string that is formed is GGBBBB. Therefore it would emit 2 G nemes for every 4 Bnemes. To continue one step further , the GGBBBB string has a 66% chance of exchanging with another B wave and a 33% chance of exchanging with a Bneme on a proximate String.
So the conjecture is that an iterative model based on these simple rules will make various patterns of emergence.
The further conjecture is that by controlling the variables of Freq, Amplitude, Damping and End point on Three Strings, we will be able to see and explore enough patterns of emergence to find ones that map to exchange data in the real world.
All comments are needed and welcome to refine and continue down this path.