Njournal Notes 5.0 Visualization

An nTu can be seen as a triangle. Since Nemetic code is content agnostic, in this case I will choose sender, receiver, observer to be the nodes of the triangle. I will also use Notice. Engage. Exchange as the nodes of the triangle shape.

Once visualized as a triad it is a short step to see a conversation can create connected triads which gives us a tetrahedron.

In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons) is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces.^[1]The tetrahedron is the three-dimensional case of the more general concept of aEuclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygonbase and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid".
Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.^[1]For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces.

         Wikipedia  

If we add motion to a tetrahedron we see this..




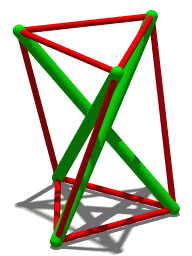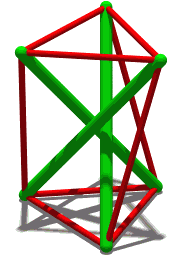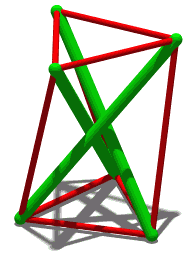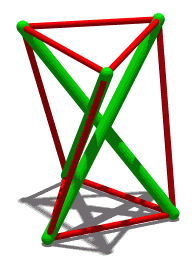
 By Cmglee (Own work) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons

We can fill in the nPlex box, with the structure above.

My conjecture is  it will be helpful to see that as the structure turns it encounters similar nPlexes in it's environment.  Since the nodes are Notice. Engage. Exchange. when a node comes close to a node in the environmental nPlex they are attracted.  Depending on the location of Notice. Engage. Exchange the attraction will be stronger. Over time a strong connection will be persistant. To the extent that it is persistent it can be called an nCell denoted by nCe.

A big thank you to +Daniel Durrant . In the comment below he point to the picture below.




TensegrTENSEGRITY